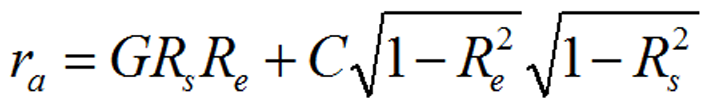Introduction [TOP]
From a very early stage in the development of his thinking about psychology, Egon Brunswik (1937) recognised the limitations of the field and its approach to knowledge. He came to realise the central role of probability in human responding (Brunswik, 1952) and later developed the conceptual framework for a study of human behaviour involving representative design (Brunswik 1955a, 1955b, 1956; Dhami, Hertwig, & Hoffrage, 2004; Hammond, 1966). The purpose of this paperi is to review and evaluate the role of probability in the thinking of Brunswik.
Egon Brunswik’s Conceptual Framework [TOP]
The conceptual framework for the study of psychology developed by Brunswik (1903-1955) unfolded from his revolutionary perspectives on the nature of psychology. To a large extent, these conceptual and methodological perspectives have been ignored, misunderstood or overlooked. In large part, they challenge the foundations of much modern psychological thought and practice. This is because they emphasise analysing the constancy of behaviours of the individual in his/her context.
Brunswik’s ideas evolved from his work on the constancy of perception, that is, the important physiological reaction of people to respond coherently to a changing world. He was amongst the first to allow for uncertainty in any given situation. This was evident in the fact that people can respond similarly to varying situations but also differently to the same situations. These views on human behaviour can be categorised under the heading of probabilistic functionalism (i.e., the study of behaviour and consciousness in adaptation). The chronology and development of how Brunswik came finally to this perspective is outlined in Table 1 and introduced in the following sections of this paper.
Despite the fact that Brunswik allowed for uncertainty, his framework was quintessentially descriptive and scientific. He introduced “…the idea of an environment that included probability relations among the variables of interest” (Hammond & Stewart, 2001, p. 3). The role of probability in the framework outlined by Brunswik arose from the fact that he acknowledged perceptions to be the outcome of an incomplete and variable processing of sensory information. Brunswik stressed that most people function in situations that are both uncertain and involve a multiplicity of cues (i.e., sources of information). Other reasons for uncertainty arose in part from the person as an imperfect judge. As a result, he viewed the relationships in terms of “…probable partial causes and partial effects” (Brunswik, 1952, p. 22) and mentioned “…the inherent probability character of object-cue and of means-end relationships” (p. 23).
An early hint to the role of probability in the thinking of Brunswik is found in the joint paper of Tolman and Brunswik (1935). In that paper they started from the premise that one situation acts as a type of discriminative stimulus and that with the effluxion of time it comes to be representative. Very quickly, they noted, however, that (a) the links were what they called “equivocal”, that is not 100 per cent reliable, and (b) that people accept some objects in the environment as the most probable representatives of the future. In a later paper (1939), Brunswik referred to a “psychophysics of probability” and a “Weber Law of probability” (Hammond & Stewart, 2001, p. 202).
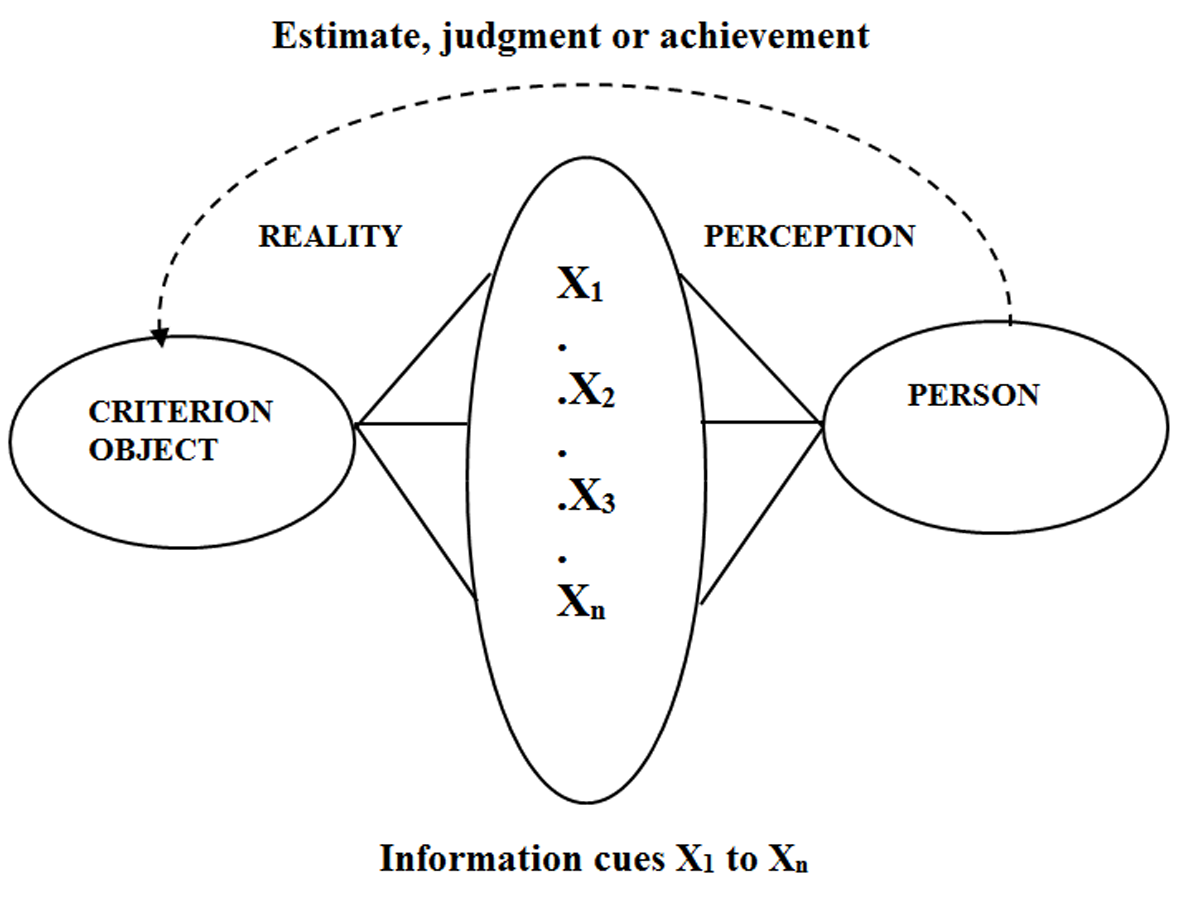
The model within which Tolman and Brunswik (1935) at first conceptualised this probability was one of goal-means and cue-means relationships. This was extended to become the lens model adapted from Heider (see Wolf, 2003). This model represented the accuracy of the perception of a criterion object (i.e., a person, event or situation) through the information provided by cues in the environment. The lens model (see Figure 1) had the advantage that it was consistent with what is called the representative design of psychological experiments. A representative design is one where a set of relevant contexts is sampled adequately. The lens model relies on varying the situations across which an individual responds. Analysing responses to varying situations allows one to determine the extent of lawfulness in a person’s behaviour. The study by Athanasou and Kaufmann (2010) gives an example of the application of the lens model approach to the mode of decision-making. It investigated the pattern of decision-making used by a single rehabilitation expert.
In this study a counsellor was given 37 accident victims’ self-ratings of health, energy, daily activities, self-esteem, personal relations, financial resources and living conditions (these are the so-called information cues - see the centre of Figure 1). The counsellor was asked to consider the self-ratings and then judge whether the quality of life of the accident victim was poor or good in each case. At the same time, the accident victim also rated his/her own overall quality of life as poor or good. The ratings of the accident victims represent the criterion (see the left-hand side of Figure 1) as they represent the reality. The overall match between the counsellor’s judgments and the accident victim’s judgments represents the achievement index. This index is the overall accuracy of the estimates. In this example, the rehabilitation expert assigned different probabilities to the cues or information than those used by the accident victims. The expert was correct in 64.8% of cases whereas using any one of the seven cues by itself would have yielded at least 54% accuracy. The pattern of decision-making was described in terms of probabilities of the relevance of cues rather than in terms of correlations of each cue with an outcome (i.e., judgment of the quality of life).
At the outset, Brunswik had cemented into his thinking a probabilistic basis for human responding. In 1941 when Brunswik gave his address at the Symposium on Psychology and Scientific Method he envisaged a system with cues that could be ranked in probability to their links with distal variables.
In his early days, Brunswik was known - and is still known - for the Brunswik ratio from his work in perception of objects. Sjöberg (1971, pp. 30-31) described the constancy ratio (CR), or Brunswik ratio (Cohen & Quinn, 1946) as: CR = (P – r)/(P-B) where CR is the constancy ratio, r is a response usually on a physical scale, B is the correct value and P is the projected value (see also Cohen & Quinn, 1946). Complete consistency is represented by a constancy ratio of 1. Cohen and Quinn (1946, p. 147) gave the following example on triangle estimation when they introduced the Brunswik ratio:
Suppose that a standard triangle is placed at 100 yards from the observing individual and that a variable triangle is placed at 50 yards. If the standard triangle is 36 feet high, and if the subject matched solely by 'objective perception,' it would be expected that the standard triangle would be matched when the variable triangle is at 18 feet. Experiments show that this is not actually the case and the match is made somewhere between 18 and 36 feet. This difference between the actual and the objective match is the result of what is known as the 'constancy effect,' or, as in this case, as 'size constancy (Cohen & Quinn, 1946, p. 147).
Similarly, from the example of the rehabilitation counsellor, the available cues or information such as health, energy, daily activities, self-esteem, personal relations, financial resources and living conditions represent B, the correct values which are needed to estimate the quality of life of accident victims represented by P. The rehabilitation counsellor’s estimation is represented by r.
The Brunswik ratio, however, has some algebraic limitations (McDonald, 1962). It should also be noted that there are “…two different computational versions of the Brunswik ratio, depending on which stimulus is identified as the standard and which the comparison” (Myers, 1980, p. 451). Notwithstanding these limitations, the general idea is that “achievement in perception depends on a probability relation, that is, on whether the cues (signs) are reliable, nonsignificant or actually misleading” (Kurz-Milcke & Innis, 2003, p. 215).
Brunswik (1943) had used probability originally in the sense of likelihood of occurrence or the chance of an event. The probability of one cue amongst all the cues could have been determined in part by its relative frequency but gradually Brunswik had also come to focus upon the correlation coefficient.
Correlation [TOP]
By 1952, the measurement of this probability was no longer the occurrence of an event (e.g., a single correct answer or an appropriate judgment) but rather “…the correlation between variables as classes…” (Brunswik, 1952, p. 23). At more than one point in his 1952 treatise, he indicated that functional validity was “measured” by the correlation coefficient. Although Brunswik was painfully exact in his writings, it meant that by 1952 he viewed probability more as a synonym for uncertainty or more accurately the unexplained variance from a correlation. In fact, he wrote that the correlation was seen as “the ultimate norm for psychology as a whole” (p. 29) and if our interpretation is correct Brunswik saw it as the metric basis for his “probabilistic functionalism” (1952, p. 29).
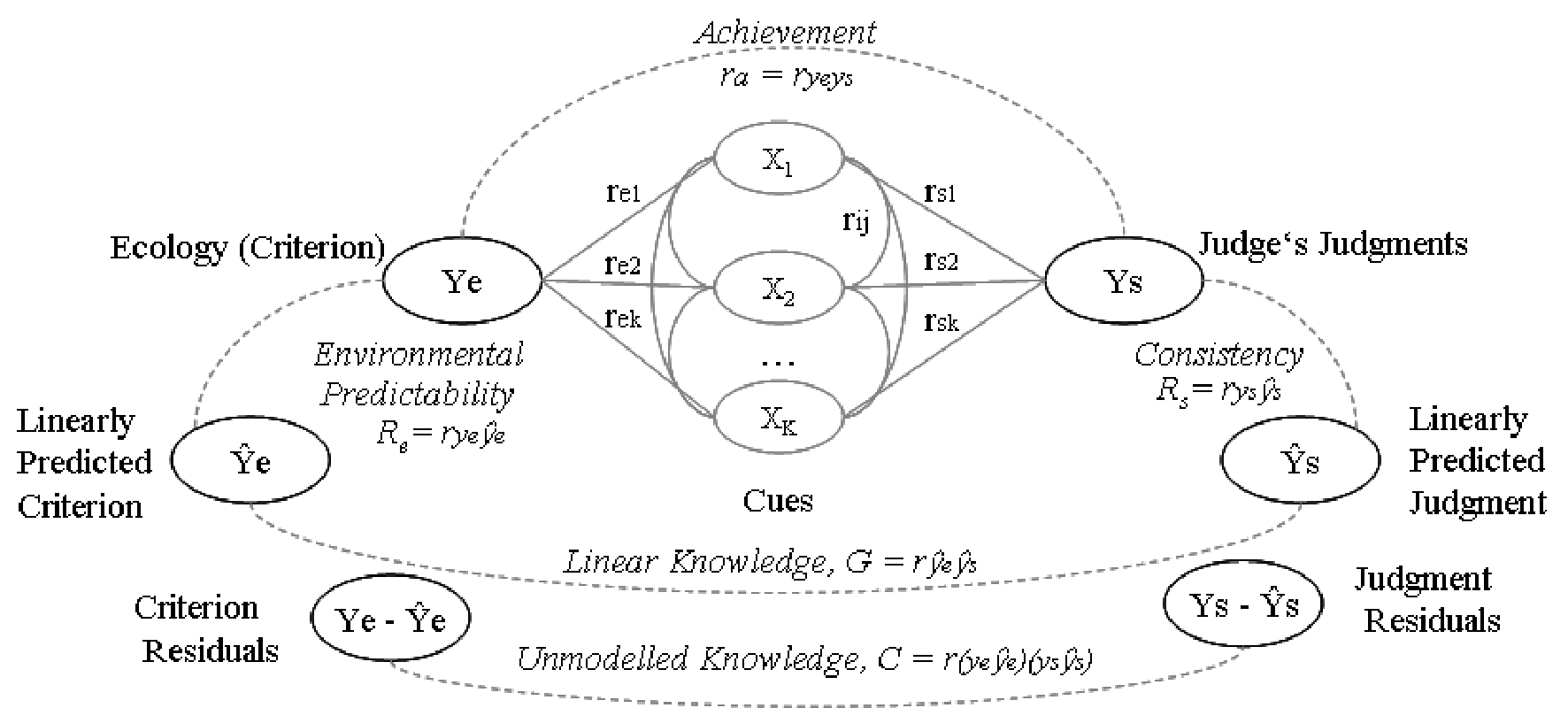
The analysis of the lens model had also changed to include correlations. In the lens model of behaviour, achievement was the correlation between repeated judgments and the criterion. This meant that it was a form of criterion validity. Within his model of functional behaviour Brunswik now considered the product-moment correlation (ra) between the initial (Ys, counsellor’s judgments) and terminal focal variable (Ye, the accident victims judgments). The cues (X1…Xn, like financial resources or living conditions) themselves may have low correlations with either focal variable. He envisaged a model of behaviour where the perception of an object and the object itself were highly correlated, that is, where the predictive or concurrent validity of an observation was high.
Since then, Tucker (1964) and the subsequent work by Stewart and Lusk (1994) unravelled the black box of Brunswik’s correlation. Tucker’s suggestion to break-down the correlation is known as Tucker’s lens model equation. Tucker’s equation includes four components which reveal a consistency, a task predictability, a linear and non-linear knowledge components (for details, Hammond & Stewart, 2001). Later, two additional bias components (conditional vs. unconditional) has been added to Tucker’s equation by Stewart and Lusk (1994) to adequately modeling categorical probability responses.
The accuracy of a response such as a judgment has been decomposed into various components through the lens model equation introduced by Hursch, Hammond, and Hursch (1964) and revised by Tucker (1964). It relies on multiple correlation and correlations between components (Cooksey, 1996). The lens model equation is a precise, mathematical identity that describes the judgment achievement (ra) of a person in terms of four components from Figure 2. Achievement (i.e., judgment performance) is equal to knowledge (G) times task predictability (Re) times consistency (Rs) plus an unmodeled component (C). Of course, it is based entirely on correlations.
where:
ra = the achievement index (i.e., the correlation between a person’s judgements and the criterion)
Re = the predictability index (i.e., the multiple correlation of the cues with the criterion)
Rs = consistency (i.e., the multiple correlation of the cues with the person’s estimates)
G = a knowledge index that is error-free achievement (i.e., the correlation between the predicted levels of the criterion and the predicted judgments)
C = an unmodeled knowledge which is the correlation between the variance not captured by the environmental predictability component or the consistency component (i.e., the correlation between the residuals from the above predictions).
Having described this historical background it is now useful to itemise - as best one can - the developments that might have occurred in Brunswik’s thinking: (a) Brunswik allowed for stray causes and effects and accordingly some uncertainty in human responding; (b) this uncertainty was indicated in a lens-type model in which judgments of a criterion were made through the lens of information or cues; (c) he equated probability with uncertainty as well as the likelihood or chance that a cue was representative of a distal criterion; (d) he used correlation as the measure of relationship or certainty; (e) the standard error of the correlation coefficient was construed as the indicator of uncertainty; (f) there was no longer any use of non-statistical measures such as the constancy ratio in his person-environment lens model. These early developments are outlined chronologically in Table 1. This traces the developments from 1935-1955 and classifies Brunswik’s ideas in terms of probability or uncertainty, together with supporting quotes.
Table 1
Chronologically Ordered Overview of Brunwik’s Ideas in Terms of Probability or Uncertainty
| Year | Author(s) | Probability theme | Comment/reference |
|---|---|---|---|
| 1935 | Tolman & Brunswik | probability of an event | |
| 1937 | Brunswik | probability of an event | “probability of success or of punishment” (Note 30) (p. 54) |
| 1939 | Brunswik | uncertainty | “In the natural environment of a living being, cues, means or pathways to a goal are usually neither absolutely reliable nor absolutely wrong” (p. 195) |
| probability of an event | “In most cases, there is objectively speaking, no perfect certainty that this or that will, or will not, lead to a certain end but only a higher or lower degree of probability” (p. 195) | ||
| 1943 | Brunswik | uncertainty | “probable partial causes and probable potential effects” (p. 58); |
| probability of an event | |||
| 1955 | Brunswik | uncertainty | |
| 1955 | Brunswik | uncertainty | “…presume, not only the legitimacy but also the necessity of the strictly descriptive or statistical disciplines…” (p. 157) |
Note. All page references are to Hammond and Stewart (2001).
It must be noted, however, that Brunswik’s conceptualisation failed to take hold in the deterministic atmosphere of 1950s psychology. Since that time, Brunswik’s ideas have enjoyed a slow but steady influence on research in a variety of areas, such as methodology (e.g., Wittmann, 1985), human-technology interaction (e.g., Kirlik, 2006), but most notably in the study of human judgment (e.g., Hammond, Hamm, & Grassia, 1986). This judgment or decision-making approach has been applied across many organisational, educational, professional and clinical settings (Karelaia & Hogarth, 2008; Kaufmann & Athanasou, 2009) and evolved as the Social Judgment Theory (Brehmer, 1988).
Typically, the studies have been idiographic in nature and based on a representative sample of situations rather than subjects. Athanasou and Kaufmann (2010) employed an N = 1 subject design but an N of many situations to study the case judgments of a rehabilitation counsellor about quality of life. This representative design of psychological experiments (i.e., an experiment in which situations and not people are sampled) is quintessentially Brunswikian (Wolf, 2005). Today, Brunswikian research is based typically on the computational lens model equation and its methods of correlation analysis (Hammond, Stewart, Brehmer, & Steinmann, 1975).
There is one sense in which this movement from relative frequency to correlations was a sad turn of events. For instance, Gigerenzer (1992, p. 12) has noted that Brunswik was influenced by American developments in descriptive statistics (e.g., correlation) and had by this time “…changed his methods from calculating (nonstatistical) ‘Brunswik ratios’…”. Possibly Brunswik preferred the correlation coefficient because it suited the representative design of psychological experiments. The problem with correlations is that they can hide as much as they reveal. Hilgard (1955) summarised the critique against Brunswik’s correlation approach in colourful terms: “Correlation is an instrument of the devil” (p. 228).
Sjöberg (1971) also went on to note that Brunswik moved on “…from the constancy ratio to the use of correlations…” (p. 48) but added that this was not justified because achievement or accuracy was no longer related to correctness or what Sjöberg termed “the full metrical correspondence…” (p. 48). Sjöberg concluded “…we do not know if the correlation coefficient constitutes a relevant measure of achievement” (p. 48). Nevertheless, correlation came to dominate the subsequent history of the person-environment model envisaged by Brunswik.
Conclusion [TOP]
What does this analysis show and how does it relate to the original ideas of Brunswik? For a start, Brunswik’s analysis and ideas came to an untimely and abrupt halt with his death in 1955. His ideas on probability and uncertainty were in a process of evolution and transition. Almost assuredly they would have been different from those outlined in Table 1. It is impossible to predict what might have been their direction or extent but it seems likely that uncertainty would have remained as a key component of the Brunswikian cosmology.
Equally, Brunswik advocated an intensive idiographic approach based on the representative sampling of cues from an ecology. He demonstrated this in the 1939 study of rat behavior. In this study rats were rewarded on the two sides of a choice situation with different probabilities representing a representative sampling approach. Finally, he showed that rats learn to discriminate the probabilities. In 1940, eight participants successfully estimated the size of cubes also in a representative sampling way. About then years later, Brunswik repeated his representative sampling approach in studies on weight illusion (1951) and Gestalt factors in photographs (1953). Had Brunswik continued his work he might have considered the psychology of the environment even further and focused on the difficulty of perceiving some arrangements of cues, rather than on the cues as individual entities.
This paper has implied that the correlation was not a suitable basis for a model that was founded originally on probability. In a sense we are proposing a return to the original Brunswik and the probability or relative accuracy of a response. This is because the correlation is not a metric of uncertainty or accuracy. At best it is a statistical index of the pattern of relationship that certainly needs additional components to reveal details of this relationship (Tucker, 1964; Stewart & Lusk, 1994).
It is possible to return to the original Brunswik. For instance, in a later paper Athanasou (2011) analysed the judgments of a rehabilitation counsellor given only partial information about the quality of life. It was concluded that the expert “…relied on the proportion or probability of accuracy rather than the correlation” (p. 95). A lens type model depicting the accuracy of case details for the judgment of the quality of life was produced. Moreover, it is acknowledged that Björkman (1967, 1973) developed a nonmetric approach to the lens model based on probabilities in order to describe judgment but as Cooksey (1996, pp. 280 et seq.) noted,“...Björkman’s model assumed that the configural information processing was non-existent...” (p. 281).
To summarise, the conceptual model of Brunswik (1955a) offers one of the most powerful experimental designs for modern psychology since it seeks to determine the lawfulness of an individual’s behavior across situations. It allows for the analysis of complex social judgments within a model in which the accuracy of a response is clearly a function of one’s perception of the situation and the intimate relationships between the factors in a situation and some criterion. It involves the intensive study of an individual in his or her contexts. This necessitates dealing with variation in behaviors or some unreliability and the appropriate measure for this is the probability of a response.
Accordingly future researchers are encouraged to commence with the representative design of a lens-type model, to sample intensively from the existing environment and to complete their analysis of individual responding using a probability approach. In short, this paper proposes that the only true psychology is one which focuses on the probability of individual responding to situations and which analyses the pattern of responding intensively. This would be consistent with the original Brunswik.

 This is an open access article distributed under the terms of the Creative Commons
Attribution License (
This is an open access article distributed under the terms of the Creative Commons
Attribution License (