Research Articles

Докладване на големина на ефекта и доверителни интервали: Преглед и начини за изчисляване

Reporting of Effect Size and Confidence Intervals: Review and Methods of Calculation

Мартин Р. Василев (Martin R. Vasilev)
[a] Университет в Потсдам, Потсдам, Германия (University of Potsdam, Potsdam, Germany).

Резюме

Въпреки критиките към тях, тестовете на статистическа значимост продължават да бъдат основната процедура за правене на статистически изводи в психологията. За да се преодолеят някои от недостатъците свързани с тях, предложено е авторите да докладват големина на ефекта и доверителни интервали като допълнителни методи за анализ на данните. Настоящата статия разглежда аргументи в полза на докладването на големина на ефекта и доверителни интервали, и проверява до колко това се прави чрез преглед на статии публикувани в български списания по психология. Резултатите показват, че мнозинството от статиите все още не докладват големина на ефекта, и че много малко статии докладват доверителни интервали. Статията след това разглежда различни мерки за големина на ефекта и начини за тяхното изчисляване. Представят се също и методи за изчисляване на доверителни интервали за големина на ефекта. Въпреки че отговорността за докладването на тези методи се пада на авторите, в статията се изразява мнението, че по-строги изисквания от страна на редакторите и преподаването на тези методи на студентите ще стимулират психолозите да променят начина, по който анализират данните си.

Ключови думи: проверка на статистическа значимост чрез нулева хипотеза, големина на ефекта, доверителни интервали, отсечки на грешката, тестове на значимост

Abstract

Despite continuous criticism, significance tests remain the main procedure for statistical inference in psychology. In order to avoid some of the problems associated with them, it has been argued that authors should report effect sizes and confidence intervals as supplemental methods of data analysis. The present article discusses arguments in favor of reporting effect sizes and confidence intervals, and investigates how common such practices are by reviewing articles published in Bulgarian psychology journals. The results show that the majority of articles still don’t report effect sizes and that very few articles report confidence intervals. The article then outlines different measures of effect size and methods for their calculation. It also presents methods for calculating confidence intervals for effect sizes. While it is ultimately the authors’ responsibility to report them, it is argued that stronger editorial policies and actively teaching these concepts to psychology students can encourage psychologists to change the way they analyze their data.

Keywords: null hypothesis significance testing, effect size, confidence intervals, error bars, significance tests

Psychological Thought, 2014, Vol. 7(1), doi:10.5964/psyct.v7i1.92

Received: 2013-09-16. Accepted: 2014-02-05. Published (VoR): 2014-04-30.

Handling Editor: Stanislava Stoyanova, Department of Psychology, South-West University "Neofit Rilski", Blagoevgrad, Bulgaria

*Corresponding author at: Am Neuen Palais 10, 14469 Potsdam, Germany. E-mail: martin.r.vasilev@gmail.com

This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/3.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Увод [TOP]

Процедурата по проверка на статистическа значимостi e най-широко използвания метод за правене на статистически изводи в психологията. Въпреки популярността си обаче, процедурата e силно противоречива и често критикувана поради методологическите ѝ ограничения и неправилното ѝ използване от изследователите (Cohen, 1994; Gigerenzer, 2004; Johansson, 2011; Loftus, 1996; Lykken, 1968; Sanabria & Killeen, 2007; Wagenmakers, 2007; за преглед виж Lambdin, 2012 и Nickerson, 2000). В следствие на тези критики са предложени алтернативни методи за анализ на данни, които да служат като допълнение на традиционните тестове за проверка на статистическа значимост.

Настоящата статия разглежда няколко популярни погрешни схващания за тестовете на статистическа значимост и обсъжда защо резултатите от тях не ни дават достатъчно информация. След това се обсъждат допълнителни методи за анализ на данни, като дискусията се фокусира върху докладване на големина на ефекта и доверителни интервали. Големината на ефекта е количествено изразяване на величината и важността на даден феномен, а доверителните интервали показват несигурността ни за истинската стойност на даден параметър на популацията (Curran-Everett, 2009; Kelley & Preacher, 2012).

В емпиричната част се представят резултатите от преглед на статии публикувани в 3 български списания по психология с цел да се провери доколко тези допълнителни методи се докладват от авторите. Накрая се дават някои практически съвети и насоки за изчисляване на големина на ефекта и доверителни интервали, и се обсъждат начини, по които да се стимулира докладването им в изследователската литература.

Погрешни интерпретации на резултатите от тестове на статистическа значимост [TOP]

Поради широката разпространеност на тестовете на статистическа значимост, доскоро беше съвсем възможно някои изследователи да прекарат цялата си научна кариера без да са използвали друг метод за статистически изводи (Andrews & Baguley, 2013). Въпреки популярността им обаче, изненадващо e колко често резултатите от тестове на статистическа значимост се интерпретират погрешно. Анонимни проучвания, които представят на студенти и професори различни твърдения относно резултати от тестове на статистическа значимост, показват че почти всички анкетирани правят поне по една погрешна интерпретация на резултатите (Haller & Krauss, 2002; Oakes, 1986). Холър и Краус например откриват, че в извадката им 100% от студентите, 89% от академичните психолози и 80% от преподавателите по методология и статистика интерпретират погрешно поне едно от шест твърдения относно резултат от тест на значимост. Погрешното интерпретиране на резултатите обаче не е характерно само за психолозите и дори опитни статистици не са имунизирани срещу него, особено при липсата на статистическа значимост (Lecoutre, Poitevineau, & Lecoutre, 2003).

Една от честите причини за погрешни интерпретации е свързана с тълкуването на p стойностите, които се получават от тестовете на статистическа значимост. Това, което p стойностите действително показват, е теоретичната вероятност, че ако две нeзависими извадки със същия размер са избрани случайно от същата популация, статистическият тест ще получи стойност толкова голяма, или по-голяма, от наблюдаваната (Nickerson, 2000). С други думи, ако едно изследване например проверява дали експерименталната група има по-бързо време на реакция от контролната група, p стойността ще покаже каква е вероятността, ако се изтегли втора случайна извадка със същия размер от същата популация, че ще се получи стойност на статистическия тест (напр. Т test), която е също толкова голяма, или по-голяма, от наблюдаваната.

P стойностите обаче често се интерпретират по различни погрешни начини: 1) като вероятността за грешка ако нулевата хипотеза е отхвърлена; 2) вероятността, че нулевата хипотеза е вярна с оглед на данните; 3) вероятността, че резултатът ще бъде репликиран при същите условия; 4) или че p стойностите показват големината на ефекта (т.е, по-ниски p стойности показват по-голям ефект; Kline, 2004). Всяка от тези интерпретации се основава на различни погрешни вярвания и интересуващите се читатели могат да ги прочетат в Kline (2004, стр. 63-68). За целите на дискусията ще бъде разгледано единствено четвъртото вярване- че p стойностите показват големината на ефекта. Тестовете на значимост са критикувани и на други основания, освен погрешната интерпретация, но те няма да бъдат разглеждани тук, защото не са централни за настоящата дискусия (напр. виж Cohen, 1994).

Допълнителни методи за анализ на резултати от тестове на статистическа значимост [TOP]

Големина на ефекта — Нека да се върнем към примера за изследването с време на реакция. Ако един експериментатор проведе такова изследване и след сравняване на средните стойности на експерименталната и контролната група получи определена p стойност, защо сама по себе си тя не може да се използва за оценка на големината на ефекта? Причината е, че тестовете на статистическа значимост и съответстващите им p стойности зависят както от големината на извадката, така и от големината на ефекта. По този начин, пренебрежително малък ефект може да стане статистически значим, ако извадката е достатъчно голяма (Kline, 2004). Тази зависимост от големината на извадката е и причината защо p стойностите не могат да се използват сами по себе си за оценка на големината на ефекта. Тестът може да покаже, че няма статистически значими разлики между средните стойности на експерименталната и контролната група, но това не означава, че силата на ефекта също е незначителна- възможно е просто изследването да няма достатъчна статистическа мощност, която да разкрие ефект, когато има такъв (виж Maxwell, 2004).

За да се преодолее този проблем е необходимо докладването на големина на ефекта (American Psychological Association [APA], 2009; Chow, 1988; Hedges, 2008; Kelley & Preacher, 2012; Volker, 2006; Wilkinson & Task Force on Statistical Inference, 1999). Големината на ефекта описва размерa на наблюдавания ефект и е подходящa за определянето на практичната и теоретичната му стойност. Изследвания със същите описателни характеристики (като средна стойност и стандартно отклонение) ще имат еднаква големина на ефекта, без значение от размера на извадката и дали получените различия са статистически значими. Поради тази причина и докладваната големина на ефекта може да бъде използвана в бъдещи мета-анализи и при определяне на статистическата мощност на последващи изследвания (Fritz, Scherndl, & Kühberger, 2013; Volker, 2006).

Ползата от докладването на големина на ефекта е съществена, защото по този начин е възможно да се определи каква е практическата значимост на резултатите. Получената статистическа значимост от даден тест не ни казва много извън това каква е вероятността резултатите да се дължат на случайна флуктуация в извадката. Практическата значимост, от друга страна, се отнася до това дали резултатът е полезен в истинския свят (Kirk, 1996). Поради тази причина, статистическата значимост не трябва да се бърка с практическата значимост.

Въпреки това обаче, в литературата лесно могат да се намерят много примери за статии, в които авторите дискутират значимостта на резултатите си единствено чрез получените p стойности. Статистическата значимост не винаги предполага и практическа значимост, но психолозите често интерпретират статистически значими резултати в дискусията като важни, големи и много значими (Cohen, 1994). Това е един парадокс, защото p стойностите сами по себе си не ни казват това, което наистина искаме да знаем- каква е големината на наблюдавания ефект и каква е неговата практическа стойност? Поради тази причина е необходимо големината на ефекта да се докладва заедно с получената статистическа значимост.

Доверителни интервали — Друг проблем, свързан с процедурата за проверка на статистическа значимост, е че тя е ориентирана към правене на дихотомни решения- нулевата хипотеза или се отхвърля или не се отхвърля (Fidler & Cumming, 2007). В следствие на това, изследователите формулират теории по отношение на това дали дадени променливи имат ефект върху други променливи. В най-добрия случай може да има предсказване на посоката, но не и точкова оценка на параметъра на популацията или прецизността на тази оценка (Cumming & Fidler, 2009).

Поради тази причина се препоръчва и докладването на доверителни интервали (APA, 2009; Cumming & Fidler, 2009; Thompson, 2002). Доверителните интервали са полезни, защото показват несигурността, която имаме при оценяване на истинската стойност на популацията по даден параметър. Например, ако изчислим доверителни интервали за средна стойност на дадена популация, можем да очакваме с определено ниво на сигурност (обикновено 95% или 99%), че истинската стойност на популацията ще попадне в този интервал. По този начин, доверителните интервали показват същата статистическа информация като p стойностите, но избягват някои от недостатъците на тестовете на значимост (Curran-Everett, 2009).

Доверителните интервали са полезни за оценка на несигурността при определяне на средната стойност на популацията и могат да бъдат представени графично като отсечки на грешката. Препоръчително е обаче доверителни интервали да се изчисляват и за докладваната големина на ефекта (Fritz, Morris, & Richler, 2012; Kelley, 2007а; Kelley & Preacher, 2012).

Отсечки на грешката — Отсечките на грешката се използват при графично изобразяване на данни и най-често могат да показват доверителни интервали, стандартна грешка или стандартно отклонение. Тук ще бъдат дискутирани само отсечки на грешката, изобразяващи доверителни интервали, защото те имат най-голямо отношение към проблемите дискутирани в тази статия.

Визуалното представяне на доверителни интервали на средни стойности може да се използва за бърза и лесна оценка на степента, до която получените средни стойности от извадката могат да се вземат „на сериозно” за определяне на средните стойности на популацията (Fidler & Loftus, 2009). Голямо предимство на отсечките на грешката е, че дължината им дава визуална представа за това колко несигурност има в данните ни- по-дългите отсечки показват голяма грешка, а по-малките показват малка грешка (Cumming, Fidler, & Vaux, 2007). За да бъдат информативни обаче, отсечките на грешката сами по себе си не са достатъчни, а е необходимо в легендата да бъде обяснено и за какво се отнасят те.

Настоящо изследване — Докладването на големина на ефекта и доверителни интервали е не само препоръчително, но и необходимо, за да се избегнат някои от проблемите свързани с тестовете на статистическа значимост. Въпреки че докладването им през последното десетилетие се е увеличило, тази промяна е сравнително бавна (Cumming, Fidler, Leonard, et al., 2007). Предишните опити да се определи колко често големината на ефекта и доверителни интервали се докладват в емпирични статии обаче са извършени с анализ на англоезични списания. Поради тази причина, настоящото проучване цели да провери доколко те се докладват в български списания по психология.

Методология [TOP]

Данни [TOP]

Данните бяха събрани чрез преглед на три български списания по психология: Психологични Изследвания, Психологическа Мисъл и Българско Списание по Психология (Balgarsko Spisanie po Psihologiâ [http://bjop.wordpress.com]; Psihologični Izsledvaniâ [http://spi.free.bg]; Psychological Thought [http://psyct.psychopen.eu]). Събрани бяха всички емпирични статии публикувани между 2007 и 2012г. От списание „Психологическа Мисъл” липсваха статии публикувани между втората половина на 2009 и 2012г. поради временно прекъсване на издаването на списанието. Също така, по време на събирането и обработка на данните (Юли 2013г.), втори брой на списание „Психологични Изследвания” все още беше под печат.

През разглеждания период в „Българско Списание по Психология” са публикувани и доклади от два национални конгреса и една международна конференция. Понеже докладите не са реферирани както останалите статии, резултатите ще бъдат представени по два начина: първо, отделно за реферираните статии и след това за докладите и реферираните статии взети заедно. И трите списания са публикували емпирични статии както на български, така и на английски език.

Кодиране [TOP]

Всички емпирични статии и доклади (N = 455) бяха прегледани и кодирани за това дали използват тестове за проверка на статистическа значимост. От тях, 74.94% използваха един или повече такъв тест; от останалите статии, най-често използвани бяха описателната статистика (11.86%) и качествените методи (5.71%). От статиите, използващи тестове за проверка на статистическа значимост, бяха премахнати тези, които използват единствено корелационни или регресионни анализи (или комбинация от двете). Причината за това е, че r и R2 стойностите, които се използват за оценка на големината на ефекта, стандартно се докладват при описване на резултатите и се извеждат от повечето стандартни софтуерни пакети (пр. SPSS). При логистичната регресия, големината на ефекта се оценява чрез т.н. съотношение на шансовете (Field, 2009). Три доклада и една статия бяха изключени поради неясно докладване на резултатите.

Останалите 253 статии и доклади бяха кодирани и използвани в последващите анализи. Таблица 1 показва броя реферирани статии, кодирани през шестте години за трите списания. Таблица 2 показва броя доклади, кодирани за двата конгреса и конференцията.

Таблица 1

Брой на кодираните реферирани статии за трите списания

Брой реферирани статии 2007 2008 2009 2010 2011 2012 Общо
Психологични Изследвания 8 11 10 9 12 5 55
Психологическа Мисъл 8 3 2 --- --- 8 21
Българско Списание по Психология 6 --- 5 --- 3 2 16
Общо 22 14 17 9 15 15 92
Таблица 2

Брой кодирани доклади

Доклади Брой
5-ти Национален Конгрес по Психология (2008) 53
The South-East Regional Conference of Psychology (2009) 58
6-ти Национален Конгрес по Психология (2011) 50
Общо 161

Всички статии и доклади бяха кодирани според това дали докладват: 1) доверителни интервали, 2) големина на ефекта, 3) доверителни интервали на големината на ефекта, и 4) отсечки на грешката при графики. Отсечки на грешката бяха кодирани когато авторите докладват средни стойности в графичен вид, но не и когато представят описателна статистика под формата на графики. Статиите и докладите също бяха кодирани за това дали са написани на български (69.6%) или на английски език (30.4%). Повечето от тези на английски език (75.3%) са от международната конференция през 2009г.

Резултати [TOP]

Сравнителните анализи на данните ще бъдат представени предимно в проценти. Понеже броят на статиите в извадката е малък, не беше възможно да се направят по-фокусирани сравнения, без да се нарушат допусканията на статистическите тестове.

Големина на ефекта [TOP]

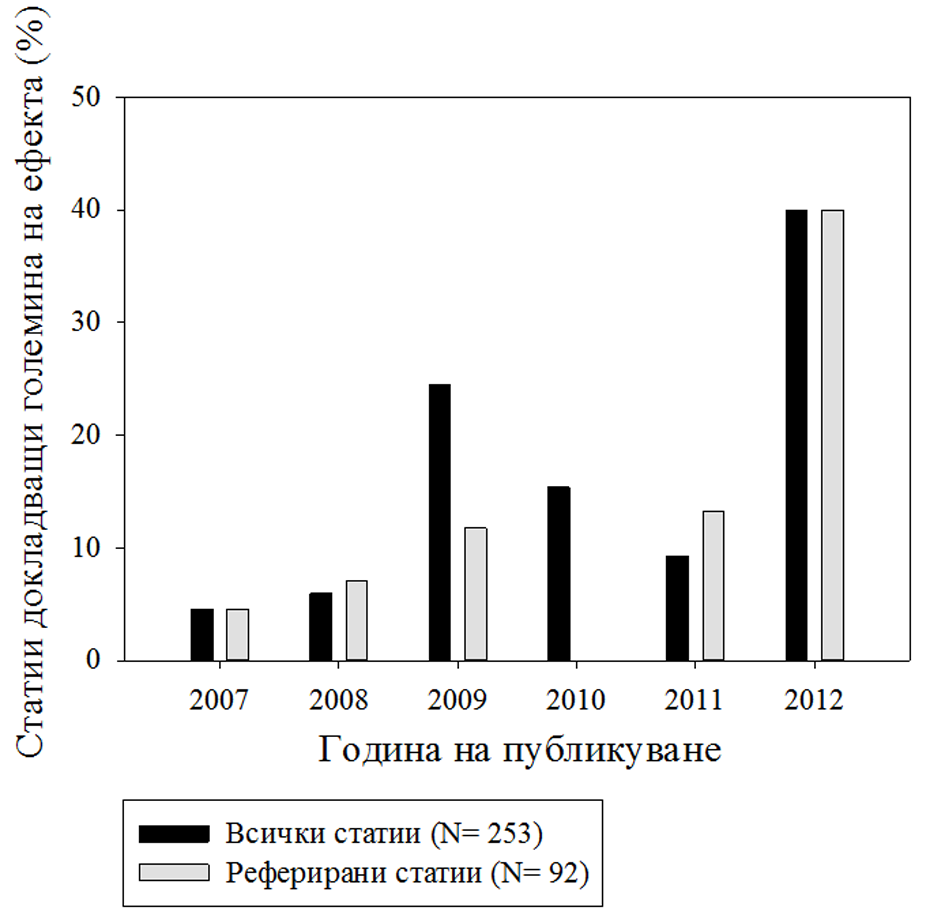
От всички кодирани статии, едва 13.43% докладват големина на ефекта за поне един статистически тест. Подобен резултат се получи и за всички реферирани статии (13.04%), и за всички доклади (13.66%), като разликата между двата типа публикации не е статистически значима, χ2 (1) = .019, p = .889, φ = .009. Коефицентът φ показва ефект с пренебрежимо малка големина. Фигура 1 представя разпределението по години на статии, докладващи големина на ефекта. При докладите, 5.66% от тях докладват големина на ефекта от конгреса през 2008г., а 8% докладват големина на ефекта от конгреса през 2011г. Процентът за конференцията през 2009г. е 25.86.

psyct.v7i1.92-f1
Фигура 1

Процент статии, докладващи големина на ефекта през шестте години.

Резултатите показват, че има увеличение в процента статии, докладващи големина на ефекта през годините, като той е най-висок през 2012г. Въпреки че скокът от 2011 до 2012г. изглежда висок, възможно е той отчасти да се дължи на малкия брой кодирани (и публикувани) статии през 2012г- едва 5.92% от всички статии и доклади.

При сравнение на статиите по език на публикация, 7.38% от всички статии и доклади на български език и 27.27% на английски език докладват големина на ефекта за поне един анализ. По този начин, публикациите на английски език по-често докладват големина на ефекта от тези на български език, като разликата е статистически значима, χ2 (1) = 18.210, p < .001, φ = .268. Коефицентът φ показва ефект с малка големина. При анализ на статиите, докладващи големина на ефекта, 55.88% от тях докладват големина на ефекта за всички проведени анализи. Също така, при повторен преглед на всички статии, докладващи големина на ефекта, едва 35.2% правят поне някакъв опит да го интерпретират в текста на статията.

Доверителни интервали [TOP]

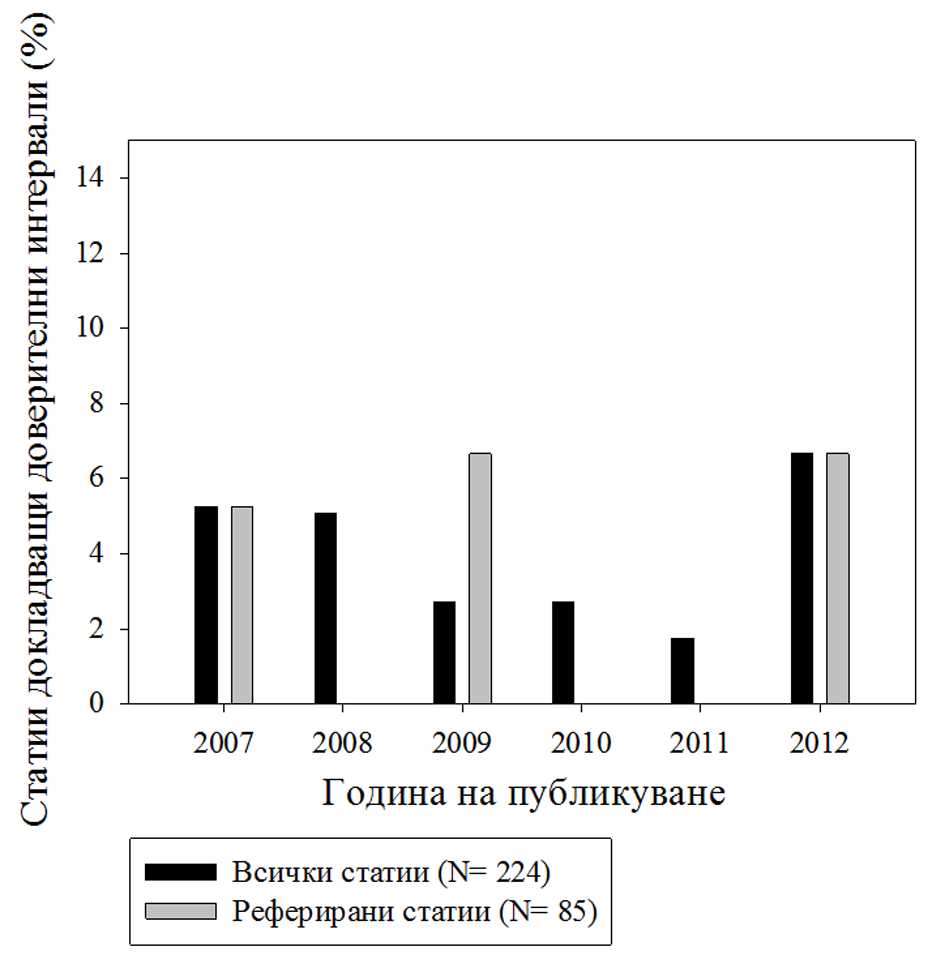
От всички статии и доклади, едва 3.57% докладват доверителни интервали за средните стойности. Фигура 2 представя разпределението по години. Също така, в нито една от статиите, докладващи големина на ефекта, не бяха изчислени доверителни интервали за него.

psyct.v7i1.92-f2
Фигура 2

Процент статии, докладващи доверителни интервали за шестте години.

На конгреса през 2008г., 6% от статиите докладват доверителни интервали за средните стойности, а на конгреса в 2011г.- 5.66%. На конференцията през 2009г процентът е 1.72

Отсечки на грешката [TOP]

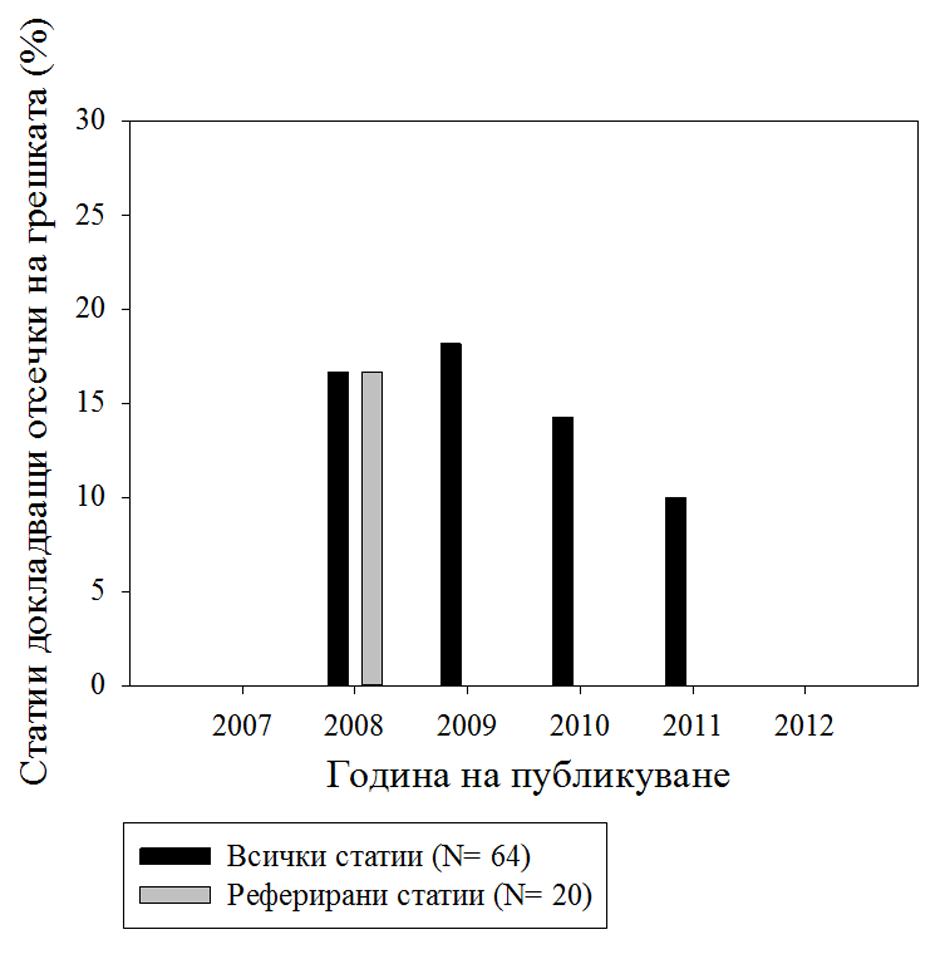
От всички статии и доклади, изобразяващи средни стойности чрез графики (N = 64), едва 12.5% имат отсечки на грешката. Разпределението по години е показано на Фигура 3.

psyct.v7i1.92-f3
Фигура 3

Процент статии, докладващи отсечки на грешката за шестте години.

От осемте статии, докладващи отсечки на грешката обаче, само 5 споменават експлицитно какво отразяват отсечките (три статии показват доверителни интервали, една показва стандартна грешка и една показва стандартно отклонение).

Дискусия [TOP]

Целта на настоящото проучване беше да провери степента, до която авторите на статии в български списания докладват големина на ефекта и доверителни интервали. Резултатите показват, че за шестте години малко публикувани статии докладват големина на ефекта. Въпреки че процентът се увеличава с годините, все още по-малко от половината статии през 2012г. докладват големина на ефекта.

През 2012г. се наблюдава по-голямо увеличение на статиите, докладващи големина на ефекта, в сравнение с предходните години. Възможно е това да отразява промяна в желаната посока. От друга страна обаче, възможно е и процентите за някои години да са изкуствено завишени или занижени поради малкото кодирани статии. Поради тази причина, разпределението по години трябва да се разглежда по-скоро като приблизително.

Проверката за статии, докладващи доверителни интервали, показва, че те почти не се докладват; също така, процентът на статии, докладващи доверителни интервали, варира през годините и не се открива някаква ясна времева тенденция. Подобен резултат се получи и за статиите, изобразяващи отсечки на грешката, въпреки че процентът е малко по-висок от статиите докладващи доверителни интервали. Като цяло не се наблюдават разлики между публикуваните реферирани статии и доклади. Това подсказва, че редакторските колективи и рецензентите на списанията през тези години вероятно не са оказали забележимо въздействие върху докладването на големина на ефекта и доверителни интервали.

Tези резултати се различават от други проучвания на статии, публикувани в англоезични списания, които откриват, че средно 38.4% от статиите докладват големина на ефекта и 10.4% докладват доверителни интервали (Fritz, Scherndl, & Kühberger, 2013). Това предполага, че статиите, публикувани в български списания, по-рядко докладват големина на ефекта и доверителни интервали в сравнение с англоезичните списания. Това заключение се подкрепя и от анализа на статии публикувани на български и английски език- тези публикувани на английски език докладват по-често големина на ефекта.

Въпреки че докладването на големина на ефекта е важно, в повечето случаи е необходимо и той да се интепретира при дискутирането на резултатите (Kelley & Preacher, 2012). Едва около една трета от статиите с големина на ефекта обаче правят това в настоящата извадка. Затова, освен самото докладване на големината на ефекта, важно е да бъде обсъдено и какво означава той в контекста на изследването. Също така, препоръчително е и да се изчисляват доверителни интервали за големината на ефекта (Kelley, 2007a). В настоящото проучване обаче, в нито една статия, докладваща големина на ефекта, не бяха изчислени и доверителни интервали за него.

В остатъка от статията ще бъдат обсъдени накратко някои по-често използвани индекси за големина на ефекта и начини за изчислението им. Ще се обсъдят и начини за изчисляване на доверителни интервали. Целта не е да се направи изчерпателен обзор на литературата, а по-скоро да се изведе на едно място най-съществената информация за изчисляване на големина на ефекта и доверителни интервали. За по-подробен обзор, читателите могат да се обърнат към Kline (2004) и Grissom и Kim (2005).

Индекси за големина на ефекта: видове и изчисляване [TOP]

Индексите за големина на ефекта могат да се разделят най-общо на две групи или „семейства”: разлики между групи (d семейство) и мерки на асоциация (r семейство; Ellis, 2010). В тази секция ще бъдат представени някои по-често използвани индекси и начини за тяхното изчисление.

Разликa между групи (d семейство) — Индексите от d семейството са подходящи за експериментални дизайни, където има сравнение на две групи и където зависимата променлива е непрекъсната, а независимата е категориална (Nakagawa & Cuthill, 2007). Трите най-често използвани индекси от тази група са представени в Таблица 3. Индексите се различават единствено по знаменателя си, понеже има повече от един начин, по който може да се определи стандартното отклонение на полулацията (Kline, 2004). Делта на Глас (Δ) използва единствено стандартното отклонение на контролната група и поради тази причина е по-подходящ, ако се смята, че експерименталната манипулация е изкривила разпределението по някакъв начин (Fritz, Morris, & Richler, 2012).

Таблица 3

Индекси за големина на ефекта при параметрични тестове (d семейство)

Статистически тест Индекс Формула Пояснение Източници
T тест d на Коен (Cohen’s d) psyct.v7i1.92-m1.svg M1 - M2 е разликата в двете средни стойности; psyct.v7i1.92-m2.svg (Cohen, 1988)
T тест Делта на Глас (Δ) (Glass’ delta) psyct.v7i1.92-m3.svg Me - Mc е разликата в средните стойности на експерименталната и контролната група; SDc е стандартното отклонение на контролната група (Grissom & Kim, 2005)
T тест g на Хеджис (Hedges’ g) psyct.v7i1.92-m5.svg psyct.v7i1.92-m6.svg (Grissom & Kim, 2005)

D на Коен и g на Хеджис, от друга страна, изчисляват големина на ефекта чрез обединяване на стандартното отклонение на двете групи. G на Хеджис представлява модификация на d на Коен, и въпреки че не е много добър предиктор на стандартното отклонение на популацията, той представлява по-стандартизирана мярка от другите два индекса в тази група (Ferguson, 2009). В някои случаи обаче, d на Коен и g на Хеджис имат склонност да надценяват съответния параметър: колкото по-малка е извадката и колкото по-голям е ефектът на популацията, толква повече се увеличава позитивното изкривяване (Grissom & Kim, 2005). G на Хеджис e по-малко склонен към това изкривяване в сравнение с d на Коен. Също така, според Клайн (Kline, 2004), g на Хеджис като цяло е по-полезният от двата индекса.

Измерване на сила на взаимовръзката (r семейство) — Най-често използваните индекси в това семейство са представени в Таблица 4. Посочените индекси могат да се използват както за корелационни, така и за експериментални дизайни (Snyder & Lawson, 1993).

Таблица 4

Индекси за големина на ефекта при параметрични тестове (r семейство)

Статистически тест Индекс Формула Пояснение Източници
Дисперсионен анализ (еднофакторен / двуфакторен) Ета на квадрат (psyct.v7i1.92-m7_HTML.svg)
(Eta squared) 		psyct.v7i1.92-m8.svg SSBetween e сбор на квадратите между групите; SSTotal e цялостен сбор на квадратите (Shaughnessy, Zechmeister, & Zechmeister, 2012)
Дисперсионен анализ (еднофакторен / двуфакторен) Частична Ета на квадрат (psyct.v7i1.92-m9_HTML.svg)
(Partial eta squared) 		psyct.v7i1.92-m10.svg SSError e грешката на сумата на квадратите (Levine & Hullett, 2002)
Дисперсионен анализ (еднофакторен) Епсилон на квадрат (psyct.v7i1.92-m11_HTML.svg) (Epsilon squared) psyct.v7i1.92-m12.svg df e степените на свобода; MSError e среден квадрат на грешката; SS е сбор на квадратите (Snyder & Lawson, 1993)
Дисперсионен анализ (еднофакторен / двуфакторен) Омега на квадрат (psyct.v7i1.92-m13_HTML.svg) (Omega squared) psyct.v7i1.92-m14.svg (Snyder & Lawson, 1993)
Дисперсионен анализ (еднофакторен / двуфакторен) Частична Омега на квадрат (psyct.v7i1.92-m15_HTML.svg) (Partial omega squared) psyct.v7i1.92-m16.svg (Olejnik & Algina, 2003)
Дисперсионен анализ (еднофакторен) ƒ на Коен (Cohen’s ƒ) psyct.v7i1.92-m17.svg η2 е Ета на квадрат (Cohen, 1988)
Множествена регресия/
Йерархична множествена регресия* 		ƒ2 на Коен (Cohen’s ƒ2) psyct.v7i1.92-m18.svg
psyct.v7i1.92-m19.svg		 R2 e коефициентът на детерминация; RB e променливата от интерес, а RA е групата от всички останали променливи (Selya, Rose, Dierker, Hedeker, & Mermelstein, 2012)

Бележка: „Шапката” (psyct.v7i1.92-m20_HTML.svg) над гръцките букви означава, че индексът се отнася за извадката; индексите без нея се отнасят до параметъра на популацията (Kline, 2004). В статията се обсъжда големина на ефекта за извадката, но той също така може да бъде изчислен и за популацията.

Ета на квадрат (eta_squared.svg) е един традиционен индекс за измерване на силата на асоциация, който обаче има известни проблеми понеже проявява позитивно изкривяване и е склонен да надценява ефекта на популацията (Grissom & Kim, 2005). Един вариант на този индекс е частичната Ета на квадрат (eta_squared_partial_HTML.svg), която се изчислява от SPSS. В по-старите версии на програмата индексът е докладван като eta_squared.svg, но това сега е поправено (Levine & Hullett, 2002). Сравнително честа практика при двуфакторен дисперсионен анализ e да се докладва eta_squared.svg за цялостния ефект и eta_squared_partial_HTML.svg за индивидуалните ефекти (Kline, 2004).

Епсилон на квадрат (epsilon_squared_HTML.svg) e друг индекс подобен на eta_squared.svg, който като цяло се смята, че показва по-малко изкривяване при определяне на големината на ефекта (Grissom & Kim, 2005). Омега на квадрат (omega_squared_HTML.svg) също има по-малко изкривяване при определяне на обяснената вариация на популацията в сравнение с eta_squared.svg. Двата индекса започват да клонят към една и съща стойност с увеличаването на размера на извадката и затова omega_squared_HTML.svg е за предпочитане при по-малки извадки (Kline, 2004). Характерно за omega_squared_HTML.svg също е, че определя големината на ефекта на популацията, вместо този на самото изследване (Fritz, Morris, & Richler, 2012). Един вариант на omega_squared_HTML.svg е частичната Омега на квадрат (omega_squared_partial_HTML.svg). Разликата му се състои в това, че измерва силата на ефекта като отношение на вариацията, която не може да бъде преписана на други ефекти (Grissom & Kim, 2005). Както omega_squared_HTML.svg получава по-малко изкривени резултати в сравнение с eta_squared.svg, така и реултатите на omega_squared_partial_HTML.svg са по-малко изкривени в сравнение с eta_squared_partial_HTML.svg.

ƒ2 на Коен е подходящ за изчисляване на големината на ефекта при множествена регресия, когато независимата и зависимата променлива са непрекъснати. Този индекс може да се използва и при йерархична множествена регресия. ƒ2 на Коен може да се изчисли и със статистическата програма SAS (виж Selya et al., 2012). Вариация на този индекс, ƒ на Коен, може да се използва и за еднофакторен дисперсионен анализ. Както се вижда на Таблица 4, ƒ на Коен може да се изведе лесно след като е изчислен eta_squared.svg.

Непараметрични тестове и анализ на други типове данни — Докладването на големина на ефекта за непараметрични тестове понякога се пренебрегва, но то е също толкова важно, колкото и за параметрични тестове. За тестовете на Ман Уитни и Уилкоксън, големината на ефекта може да се изчисли с помощта на z стойността, която се извежда от статистически пакети като SPSS (Fritz, Morris, & Richler, 2012; виж Таблица 5).

Таблица 5

Индекси за големина на ефекта при непараметрични и други видове тестове

Статистически тест Индекс Формула Пояснение Източници
Тест на Ман Уитни/ Уилкоксън (Mann-Whitney/Wilcoxon test) r psyct.v7i1.92-m39.svg z e стойността от теста; N e броят наблюдения (Fritz, Morris, & Richler, 2012)
χ2 тест ϕ коефици-ент psyct.v7i1.92-m40.svg χ2 е стойността от теста; N e броят наблюдения (Chedzoy, 2006)
χ2 тест (>2x2 таблица) V на Крамéр (Cramér's V) psyct.v7i1.92-m41.svg k e броят редове или колони (по-малката от двете стойности) (Cramér, 1946)
N/A Съотношение на шансовете (Odds Ratios) psyct.v7i1.92-m42.svg А = [+ излагане, + изход];
B = [+ излагане, - изход];
C = [- излагане, + изход];
D = [- излагане, - изход] 		(Szumilas, 2010)

При категориални данни анализирани с χ2 тест, големината на ефекта може да се изчисли с няколко индекса. Коефицентът ϕ е подходящ когато данните се анализират като 2x2 таблица. Когато таблицата е по-голяма (т.е. има повече от две колони или редици), по-подходящо е да се използва модифицирания индекс V на Крамéр. Трети индекс, ламбда на Гудман и Крускълс (λ) (Goodman and Kruskal's lambda), пък се използва когато има предсказване на резултат при категориални променливи. Той измерва пропорционалното увеличаване на правилното предсказване на изхода за една категориална променлива, когато имаме информация за втора категориална променлива. Например, бихме могли да проверим доколко способността ни да предскажем дали студентите ще си вземат или няма да си вземат изпита се определя от това, че знаем пола им (Cramer & Howitt, 2004). И трите индекса за големина на ефекта могат да бъдат изчислени от SPSS, ако са избрани като опция.

Друг индекс на големина на ефекта е т.н. съотношение на шансовете. То като цяло има по-широко приложение в медицината, но е приложимо и в психологията при биномиални данни. Съотношението на шансовете се използва за сравнение на относителната вероятност на изхода, от който се интересуваме (например болест или разстройство), при излагане на променливата от интерес (за повече информация виж Szumilas, 2010).

Калкулатори за големина на ефекта [TOP]

Въпреки че не всички индекси могат да се изчисляват от повечето статистически пакети, съществуват някои онлайн калкулатори, които могат да спестят ръчното смятане по формулите. С калкулаторът на Wilson (n.d.) могат да се изчислят голям брой индекси, включително и повечето обсъждани тук. Други полезни калкулатори са на Ellis (2009) и Lyons и Morris (2013).

Докладване на големина на ефекта [TOP]

Според насоките на Американската Психологическа Асоциация, „почти винаги [e] необходимо да се включи някаква мярка на големината на ефекта при резултатите” (APA, 2009, стр. 34). Както беше описано досега, съществуват различни индекси, по които може да се изчисли големината на ефекта, а при някои дизайни има избор между повече от един индекс.

Тъй като различните индекси се изчисляват по различен начин, получените стойности не винаги са еквиваленти и могат да се тълкуват по един и същ начин. Поради тази причина, важно е при докладването на големина на ефекта да се спомене чрез кой точно индекс е изчислен (Ellis, 2010). Индексите от d семейството могат да се преобразуват в индекси на силата на асоциация (и обратно) по следните формули (Ferguson, 2009):

(1)
psyct.v7i1.92-m43.svg

(2)
psyct.v7i1.92-m44.svg

Cohen (1988) въвежда няколко критерия за оценка на ефектите като „малки”, „средни” и „големи” (виж също Cohen, 1992; Ellis, 2010, cтр. 40-42). Например, за d на Коен, стойност от .20 показва малък ефект, .50 показва умерен ефект и .80 показва голям ефект. Тези критерии са полезни, защото водят до по-лесно сравняване на големината на ефекта в различни изследвания. Въпреки това, според някои изследователи критериите са противоречиви и като цяло е препоръчително големината на ефекта да се интерпретира в контекста на изследователската област (Ellis, 2010; Zakzanis, 2001).

Изчисляване на доверителни интервали [TOP]

Доверителните интервали за средни стойности могат да бъдат изведени лесно със стандартните статистически пакети и затова изчисляването им няма да бъде дискутирано тук (формули могат да бъдат намерени в Cumming & Fidler, 2009). Изчисляването на доверителните интервали за големина на ефекта обаче не е същото като доверителните интервали за параметри като средна стойност и стандартно отклонение (Thompson, 2002). Като цяло, тези доверителни интервали се изчисляват по-трудно, защото зависят от нецентралните t, F и χ2 разпределения (Kelley, 2007a). Cumming (2012) предлага Excel макроси (като допълнение към книгата си), с които могат да се изчисляват доверителни интервали на d и r индекси. Самите макроси са със свободен достъп и могат да се използват и без книгата (виж Cumming, n.d.). Kelley (2007a) пък описва скриптове за изчисляване на доверителни интервали за големина на ефекта с помощта на MBESS- пакет за програмата R (виж Kelley, 2007b). Също така, калкулаторът на Wilson (n.d.) изчислява 95% доверителни интервали за индексите.

Стимулиране на докладването на големина на ефекта и доверителни интервали [TOP]

Промяната в начина на анализиране на данните е необходима, за да се избегнат някои от недостатъците на тестовете за проверка на статистическа значимост (Loftus, 1996). Както обаче се вижда от представените данни, все още сравнително малко изследователи в България докладват големина на ефекта, а още по-малко докладват доверителни интервали. Съществуват поне два начина, по-които може да се стимулира докладването им от изследователите.

Първо, създаването на редакторски указания от реферираните списания в България ще доведе до увеличаване на процента автори, докладващи големина на ефекта и доверителни интервали. Тези указания биха могли да се разширят и до рецензентите, които също да следят за докладването им. Въпреки че е възможно някои автори отново да не ги интерпретират в дискусията си (Fidler, Thomason, Cumming, Finch, & Leeman, 2004), това все пак е положителна стъпка напред.

Подобна инициатива би била още по-ефективна, ако е подкрепена и от професионалните сдружения на психолозите в България. Положителен пример в тази насока е Американската Психологическа Асоциация, която изисква докладването на големина на ефекта и доверителни интервали в списанията, публикувани от асоциацията (виж APA, 2009, стр. 33).

Друга по-обещаваща стратегия е тези допълнителни методи за анализ на данни да се преподават рутинно по време на обучението на студентите по Статистика (Schmidt, 1996). Самите студенти не са привикнали да използват механично тестовете за проверка на статистическа значимост и затова биха били по-пластични при усвояването на тези алтернативни методи (Kline, 2004). В последните няколко години са публикувани подходящи книги, които въвеждат в проблема (напр. Cumming, 2012; Ellis, 2010) и които биха могли да се изпoлзват за обучение. Публикувани са и статии, написани на по-разбираем език, които също могат да се използват за тази цел (напр. Cohen, 1990; Cumming & Fidler, 2009; Cumming & Finch, 2005; Hedges, 2008).

Заключение [TOP]

Въпреки широкото си разпространение, процедурата за проверка на статистическа значимост не е без своите недостатъци и резултатите от нея често са интерпретирани погрешно. За да се избегнат някои от тези проблеми, е необходимо да се използват допълнителни методи за анализ на данни, като изчисляване на големина на ефекта и доверителни интервали. Подобно на предишни проучвания в англоезичната литература, анализът на публикувани статии в три български списания по психология показа, че тези два метода се докладват рядко и почти не се обсъждат в дискусията. Промяната към докладването им е не само желателна, но и необходима стъпка, защото така ще се подобрят значително сегашните практики за анализ и интерпретация на данни, и присъщите им недостатъци.

Бележки [TOP]

i) В литературата тази процедура се нарича „Проверка на статистическа значимост чрез нулева хипотеза” (Null hypothesis significance testing; Nickerson, 2000). За улеснение обаче, в статията ще бъде използван съкратения термин „проверка на статистическа значимост”.

Финансиране [TOP]

Авторите не са получили финансиране, което да докладват.

Конфликт на интереси [TOP]

Авторите декларират, че не съществува конфликт на интереси.

Благодарности [TOP]

Авторите не са получили помощ/подкрепа, която да докладват.

Литература [TOP]

  • American Psychological Association. (2009). Publication manual of the American Psychological Association (6th ed.). Washington, DC: Author.

  • Andrews, M., & Baguley, T. (2013). Prior approval: The growth of Bayesian methods in psychology [Editorial]. British Journal of Mathematical and Statistical Psychology, 66, 1-7. doi:10.1111/bmsp.12004

  • Chedzoy, O. B. (2006). Phi-coefficient. In Encyclopedia of statistical sciences (Vol. 9, pp. 6115-6115). Hoboken, NJ: John Wiley & Sons.

  • Chow, S. L. (1988). Significance test or effect size? Psychological Bulletin, 103(1), 1105-110. doi:10.1037/0033-2909.103.1.105

  • Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). Hillsdale, NJ: Lawrence Erlbaum Associates.

  • Cohen, J. (1990). Things I have learned (so far). American Psychologist, 45(12), 121304-1312. doi:10.1037/0003-066X.45.12.1304

  • Cohen, J. (1992). A power primer. Psychological Bulletin, 112(1), 1155-159. doi:10.1037/0033-2909.112.1.155

  • Cohen, J. (1994). The earth is round (p < .05). American Psychologist, 49(12), 12997-1003. doi:10.1037/0003-066X.49.12.997

  • Cramer, D., & Howitt, D. (2004). The SAGE dictionary of statistics. London, United Kingdom: SAGE.

  • Cramér, H. (1946). Mathematical methods of statistics. Princeton, NJ: Princeton University Press.

  • Cumming, G. (n.d.). ESCI – The new statistics: Estimation for better research. Retrieved from http://www.latrobe.edu.au/psy/research/projects/esci

  • Cumming, G. (2012). Understanding the new statistics: Effect sizes, confidence intervals, and meta-analysis. New York, NY: Routledge.

  • Cumming, G., & Fidler, F. (2009). Confidence intervals: Better answers to better questions. Zeitschrift für Psychologie, 217(1), 115-26. doi:10.1027/0044-3409.217.1.15

  • Cumming, G., Fidler, F., Leonard, M., Kalinowski, P., Christiansen, A., Kleinig, A., Wilson, S. (2007). Statistical reform in psychology: Is anything changing? Psychological Science, 18(3), 3230-232. doi:10.1111/j.1467-9280.2007.01881.x

  • Cumming, G., Fidler, F., & Vaux, D. L. (2007). Error bars in experimental biology. Journal of Cell Biology, 177(1), 17-11. doi:10.1083/jcb.200611141

  • Cumming, G., & Finch, S. (2005). Inference by eye: Confidence intervals and how to read pictures of data. American Psychologist, 60(2), 2170-180. doi:10.1037/0003-066X.60.2.170

  • Curran-Everett, D. (2009). Explorations in statistics: Confidence intervals. Advances in Physiology Education, 33, 87-90. doi:10.1152/advan.00006.2009

  • Ellis, P. D. (2009). Effect size calculators. Retrieved August 22, 2013 from http://www.polyu.edu.hk/mm/effectsizefaqs/calculator/calculator.html

  • Ellis, P. D. (2010). The essential guide to effect sizes: Statistical power, meta-analysis, and the interpretation of research results. New York, NY: Cambridge University Press.

  • Ferguson, C. J. (2009). An effect size primer: A guide for clinicians and researchers. Professional Psychology: Research and Practice, 40(5), 5532-538. doi:10.1037/a0015808

  • Fidler, F., & Cumming, G. (2007). Lessons learned from statistical reform efforts in other disciplines. Psychology in the Schools, 44(5), 5441-449. doi:10.1002/pits.20236

  • Fidler, F., & Loftus, G. R. (2009). Why figures with error bars should replace p values: Some conceptual arguments and empirical demonstrations. Zeitschrift für Psychologie, 217(1), 127-37. doi:10.1027/0044-3409.217.1.27

  • Fidler, F., Thomason, N., Cumming, G., Finch, S., & Leeman, J. (2004). Editors can lead researchers to confidence intervals, but can't make them think: Statistical reform lessons from medicine. Psychological Science, 15(2), 2119-126. doi:10.1111/j.0963-7214.2004.01502008.x

  • Field, A. (2009). Discovering statistics using SPSS (3rd ed.). London, United Kingdom: SAGE.

  • Fritz, A., Scherndl, T., & Kühberger, A. (2013). A comprehensive review of reporting practices in psychological journals: Are effect sizes really enough? Theory & Psychology, 23(1), 198-122. doi:10.1177/0959354312436870

  • Fritz, C. O., Morris, P. E., & Richler, J. J. (2012). Effect size estimates: Current use, calculations, and interpretation. Journal of Experimental Psychology: General, 141(1), 12-18. doi:10.1037/a0024338

  • Gigerenzer, G. (2004). Mindless statistics. Journal of Socio-Economics, 33, 587-606. doi:10.1016/j.socec.2004.09.033

  • Grissom, R. J., & Kim, J. J. (2005). Effect sizes for research: A broad practical approach. Mahwah, NJ: Lawrence Erlbaum Associates.

  • Haller, H., & Krauss, S. (2002). Misinterpretations of significance: A problem students share with their teachers? Methods of Psychological Research, 7(1), 11-20.

  • Hedges, L. V. (2008). What are effect sizes and why do we need them? Child Development Perspectives, 2(3), 3167-171. doi:10.1111/j.1750-8606.2008.00060.x

  • Johansson, T. (2011). Hail the impossible: p-values, evidence, and likelihood. Scandinavian Journal of Psychology, 52, 113-125. doi:10.1111/j.1467-9450.2010.00852.x

  • Kelley, K. (2007a). Confidence intervals for standardized effect sizes: Theory, application, and implementation. Journal of Statistical Software, 20(8), 8). Retrieved from http://www.jstatsoft.org/v20/i08

  • Kelley, K. (2007b). Methods for the behavioral, educational, and social sciences: An R package. Behavior Research Methods, 39(4), 4979-984. doi:10.3758/BF03192993

  • Kelley, K., & Preacher, K. J. (2012). On effect size. Psychological Methods, 17(2), 2137-152. doi:10.1037/a0028086

  • Kirk, R. E. (1996). Practical significance: A concept whose time has come. Educational and Psychological Measurement, 56(5), 5746-759. doi:10.1177/0013164496056005002

  • Kline, R. B. (2004). Beyond significance testing: Reforming data analysis methods in behavioral research. Washington, DC: American Psychological Association.

  • Lambdin, C. (2012). Significance tests as sorcery: Science is empirical – Significance tests are not. Theory & Psychology, 22(1), 167-90. doi:10.1177/0959354311429854

  • Lecoutre, M.-P., Poitevineau, J., & Lecoutre, B. (2003). Even statisticians are not immune to misinterpretations of null hypothesis significance tests. International Journal of Psychology, 38(1), 137-45. doi:10.1080/00207590244000250

  • Levine, T. R., & Hullett, C. R. (2002). Eta squared, partial eta squared, and misreporting of effect size in communication research. Human Communication Research, 28(4), 4612-625. doi:10.1111/j.1468-2958.2002.tb00828.x

  • Loftus, G. R. (1996). Psychology will be a much better science when we change the way we analyze data. Current Directions in Psychological Science, 5(6), 6161-171. doi:10.1111/1467-8721.ep11512376

  • Lykken, D. T. (1968). Statistical significance in psychological research. Psychological Bulletin, 70(3, Pt. 1), 3, Pt. 1151-159. doi:10.1037/h0026141

  • Lyons, L. C., & Morris, W. A. (2013). The Meta-Analysis Calculator. Retrieved on August 22, 2013 from http://www.lyonsmorris.com/ma1/

  • Maxwell, S. E. (2004). The persistence of underpowered studies in psychological research: Causes, consequences, and remedies. Psychological Methods, 9(2), 2147-163. doi:10.1037/1082-989X.9.2.147

  • Nakagawa, S., & Cuthill, I. C. (2007). Effect size, confidence interval and statistical significance: A practical guide for biologists. Biological Reviews of the Cambridge Philosophical Society, 82, 591-605. doi:10.1111/j.1469-185X.2007.00027.x

  • Nickerson, R. S. (2000). Null hypothesis significance testing: A review of an old and continuing controversy. Psychological Methods, 5(2), 2241-301. doi:10.1037/1082-989X.5.2.241

  • Oakes, M. (1986). Statistical inference: A commentary for the social and behavioral sciences. New York, NY: Wiley.

  • Olejnik, S., & Algina, J. (2003). Generalized eta and omega squared statistics: Measures of effect size for some common research designs. Psychological Methods, 8(4), 4434-447. doi:10.1037/1082-989X.8.4.434

  • Sanabria, F., & Killeen, P. R. (2007). Better statistics for better decisions: Rejecting null hypotheses significance tests in favor of replication statistics. Psychology in the Schools, 44(5), 5471-481. doi:10.1002/pits.20239

  • Schmidt, F. L. (1996). Statistical significance testing and cumulative knowledge in psychology: Implications for training of researchers. Psychological Methods, 1(2), 2115-129. doi:10.1037/1082-989X.1.2.115

  • Selya, A. S., Rose, J. S., Dierker, L. C., Hedeker, D., & Mermelstein, R. J. (2012). A practical guide to calculating Cohen’s f2, a measure of local effect size, from PROC MIXED. Frontiers in Psychology, 3(1), 1Article 111. doi:10.3389/fpsyg.2012.00111

  • Shaughnessy, J. J., Zechmeister, E. B., & Zechmeister, J. S. (2012). Research methods in psychology (9th ed.). New York, NY: McGraw-Hill.

  • Snyder, P., & Lawson, S. (1993). Evaluating results using corrected and uncorrected effect size estimates. Journal of Experimental Education, 61(4), 4334-349.

  • Szumilas, M. (2010). Explaining odds ratios. Journal of the Canadian Academy of Child and Adolescent Psychiatry, 19(3), 3227-229.

  • Thompson, B. (2002). What future quantitative social science research could look like: Confidence intervals for effect sizes. Educational Researcher, 31(3), 325-32. doi:10.3102/0013189X031003025

  • Volker, M. A. (2006). Reporting effect size estimates in school psychology research. Psychology in the Schools, 43(6), 6653-672. doi:10.1002/pits.20176

  • Wagenmakers, E.-J. (2007). A practical solution to the pervasive problems of p values. Psychonomic Bulletin & Review, 14(5), 5779-804. doi:10.3758/BF03194105

  • Wilkinson, L., & Task Force on Statistical Inference. (1999). Statistical methods in psychology journals: Guidelines and explanations. American Psychologist, 54(8), 8594-604. doi:10.1037/0003-066X.54.8.594

  • Wilson, D. B. (n.d.). Practical meta-analysis effect size calculator. Retrieved on 22th August 2013 from http://www.campbellcollaboration.org/resources/effect_size_input.php

  • Zakzanis, K. K. (2001). Statistics to tell the truth, the whole truth, and nothing but the truth: Formulae, illustrative numerical examples, and heuristic interpretation of effect size analyses for neuropsychological researchers. Archives of Clinical Neuropsychology, 16, 653-667. doi:10.1093/arclin/16.7.653

About the Author [TOP]

Martin Vasilev graduated with a Bachelor’s degree in Psychology at Sofia University “St. Kliment Ohridski”. He is currently a Master’s degree student at University of Potsdam, Germany.



Creative Commons License
ISSN: 2193-7281
Contact
Legal Notice
PsychOpen Logo